

If is identically zero then the claim is trivial, so assume that is non-zero somewhere. Proof: By subtracting a constant from (which does not affect differentiability or the derivative) we may assume that. Theorem 4 (Rolle’s theorem) Let be a compact interval of positive length, and let be a differentiable function such that. In single-variable calculus, the operations of integration and differentiation are connected by a number of basic theorems, starting with Rolle’s theorem. ( Hint: choose an that vanishes quickly at some point, say at the origin, but which also oscillates rapidly near that point.) it is equal to an everywhere defined measurable function on outside of a null set), but give an example to demonstrate that need not be continuous.Įxercise 3 Give an example of a function which is everywhere differentiable, but not continuously differentiable.

If is almost everywhere differentiable, show that the (almost everywhere defined) function is measurable (i.e. However, for now we will stick with the classical approach to differentiation.Įxercise 2 If is everywhere differentiable, show that is continuous and is measurable. analysis centred around the Lebesgue integral, and in particular allowing functions to be uncontrolled, infinite, or even undefined on sets of measure zero). Remark 1 Much later in this sequence, when we cover the theory of distributions, we will see the notion of a weak derivative or distributional derivative, which can be applied to a much rougher class of functions and is in many ways more suitable than the classical derivative for doing “Lebesgue” type analysis (i.e. If is differentiable everywhere and its derivative is continuous, then we say that is continuously differentiable.
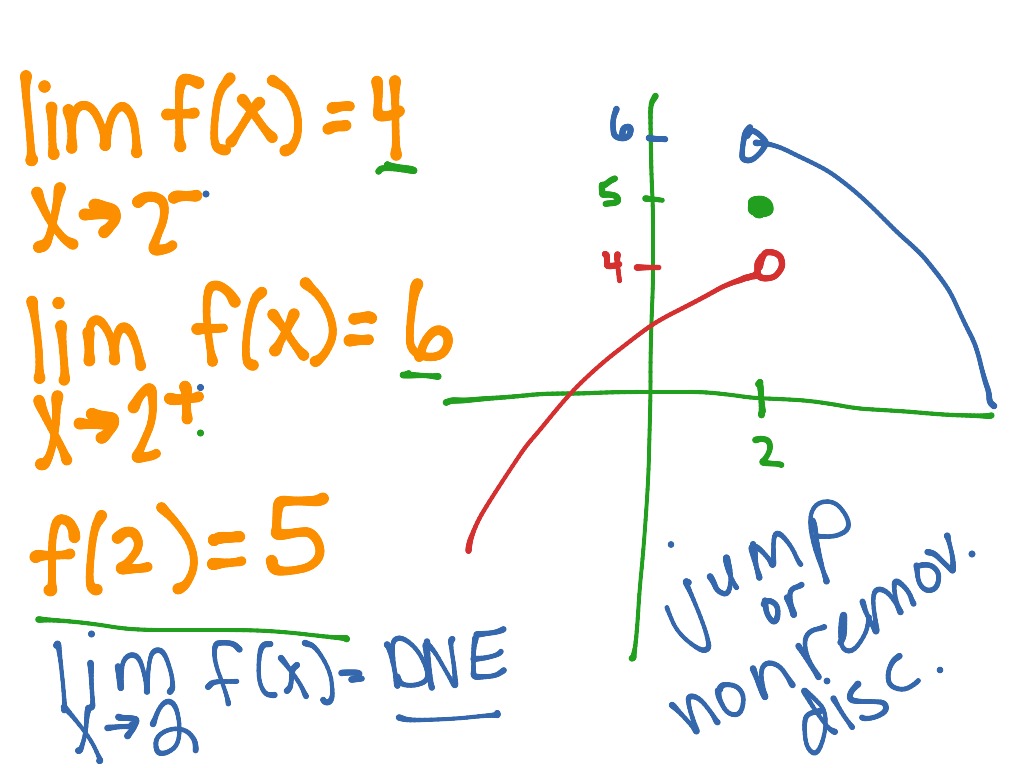
We say that is everywhere differentiable, or differentiable for short, if it is differentiable at all points, and differentiable almost everywhere if it is differentiable at almost every point. In that case, we call the strong derivative, classical derivative, or just derivative for short, of at. Recall that a function is said to be differentiable at a point if the limitĮxists. Let be a compact interval of positive length (thus ).


 0 kommentar(er)
0 kommentar(er)
